red-black Tree

A red-black tree is a binary search tree with an extra attribute colour, which can be either RED or BLACK and satisfies the red-black properties¹

• Initially known as symmetric binary B-trees
• Basic operations on a red-black tree take $O(logn)$ time in the worst case, instead of the normal $O(h)$ that normal binary_search_tree operations take.

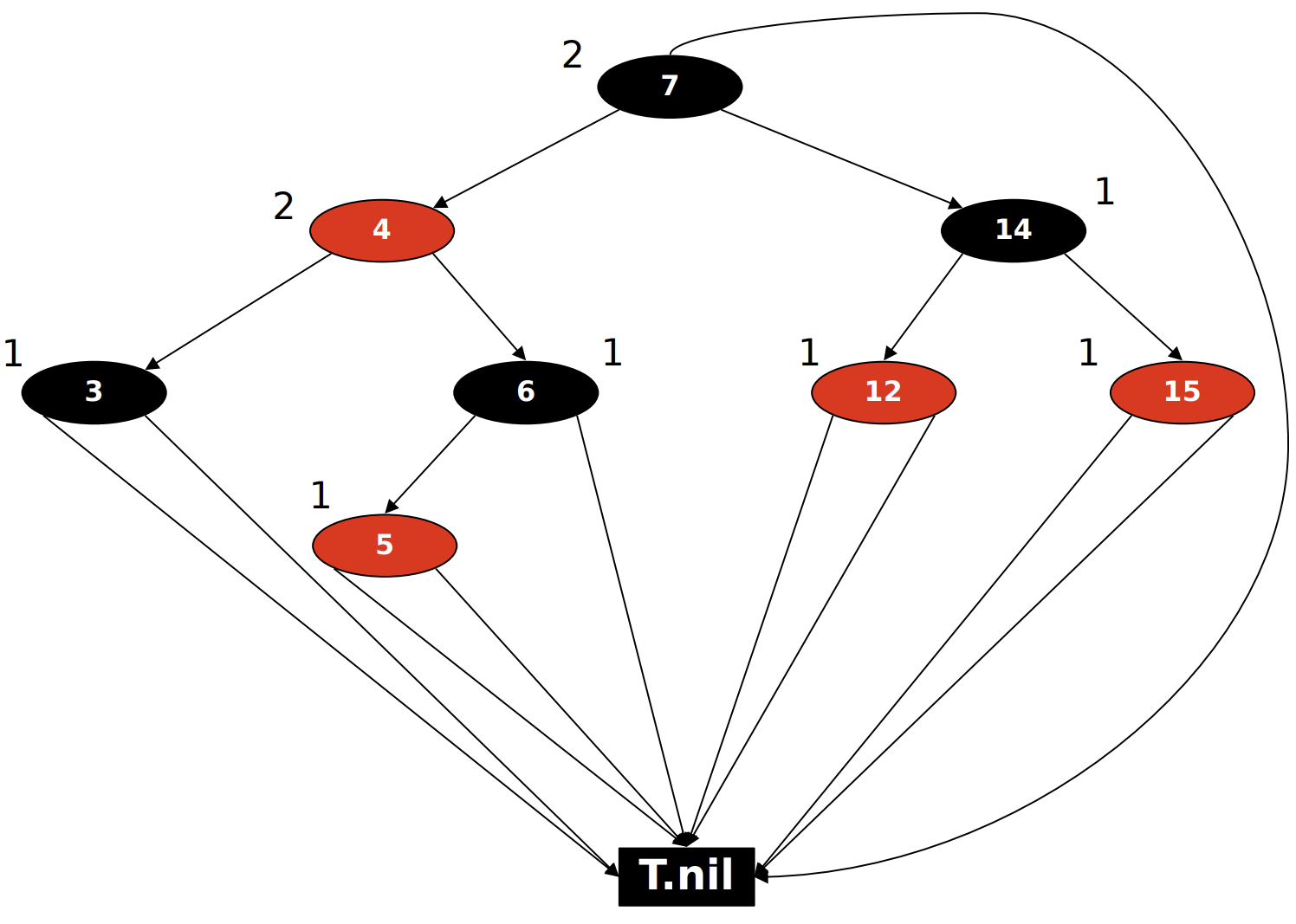
Properties

• A red-black tree with n internal nodes has height h at most 2 × log(n + 1).
• Guarantees worst-case $O(logn)$ performance for operations.
• Red nodes act as a “compression” of depth, but their number and position are controlled by strict rules.

Operations

Rotations

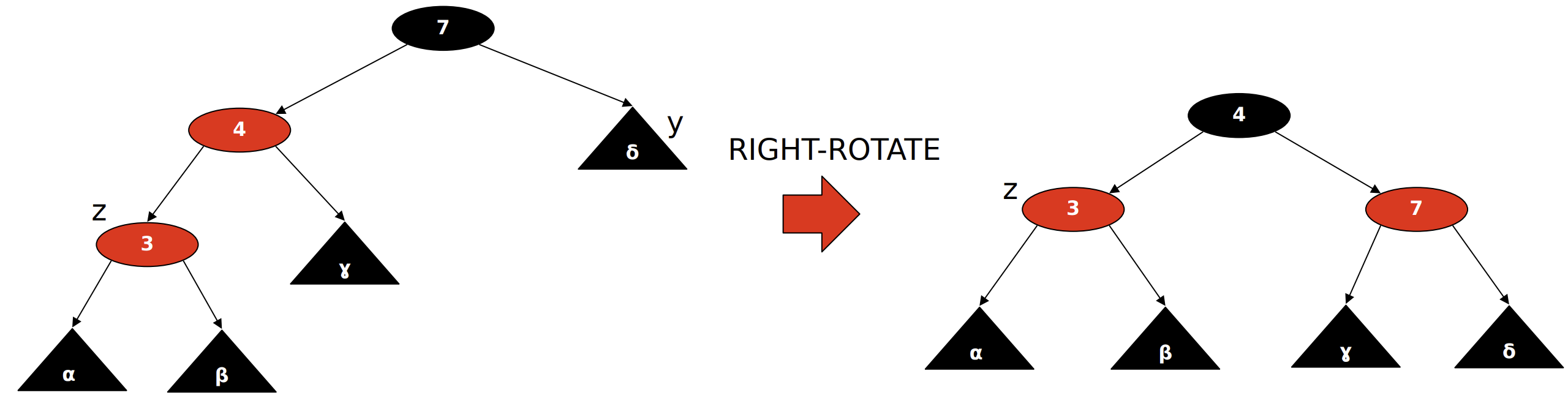
Tree rotations are local operations used to rebalance the tree:

• LEFT-ROTATE(x): Move x.right up and x down to its left.
• RIGHT-ROTATE(y): Symmetric to left-rotation.

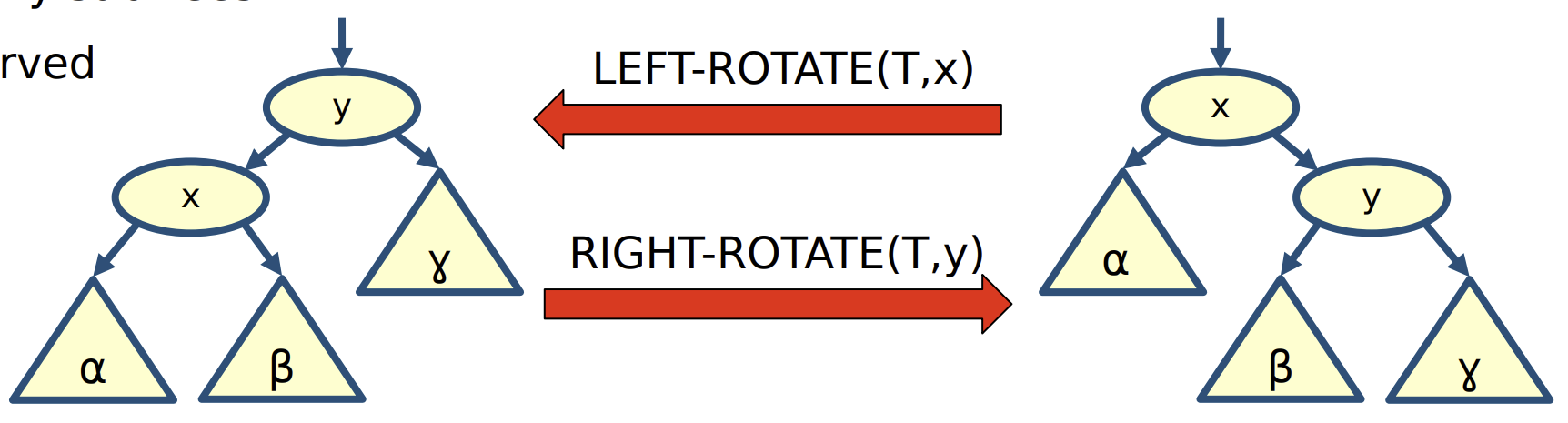
def LEFT-ROTATE(T, x): #The pseudocode for *RIGHT-ROTATE* is symmetric
    y = x.right
    x.right = y.left
    if y.left != T.nil:
        y.left.p = x
    y.p = x.p
    if x.p == T.nil:
        T.root = y
    elif x == x.p.left:
        x.p.left = y
    else:
        x.p.right = y
    y.left = x
    x.p = y

Insertion

Insertion works similarly to a standard BST, but new nodes are initially colored red. After insertion, we use FIXUP to restore the red-black properties.

def INSERT(T, z):
    y = T.nil
    x = T.root
    while x != T.nil:
        y = x
        if z.key < x.key:
            x = x.left
        else:
            x = x.right
    z.p = y
    if y == T.nil:
        T.root = z
    elif z.key < y.key:
        y.left = z
    else:
        y.right = z
    z.left = T.nil
    z.right = T.nil
    z.colour = RED
    FIXUP(T, z)

FIXUP

Fixes property violations after insertion. Cases handled:

• Case 1: z’s uncle is red → recolor parent and uncle, move up the tree.
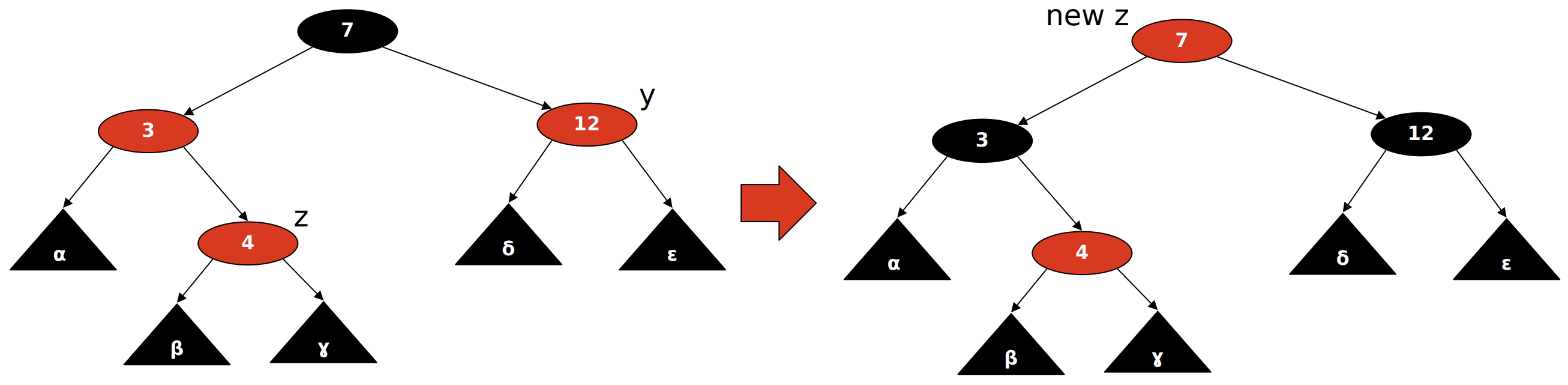
• Case 2: z is a right child and uncle is black → rotate to left.
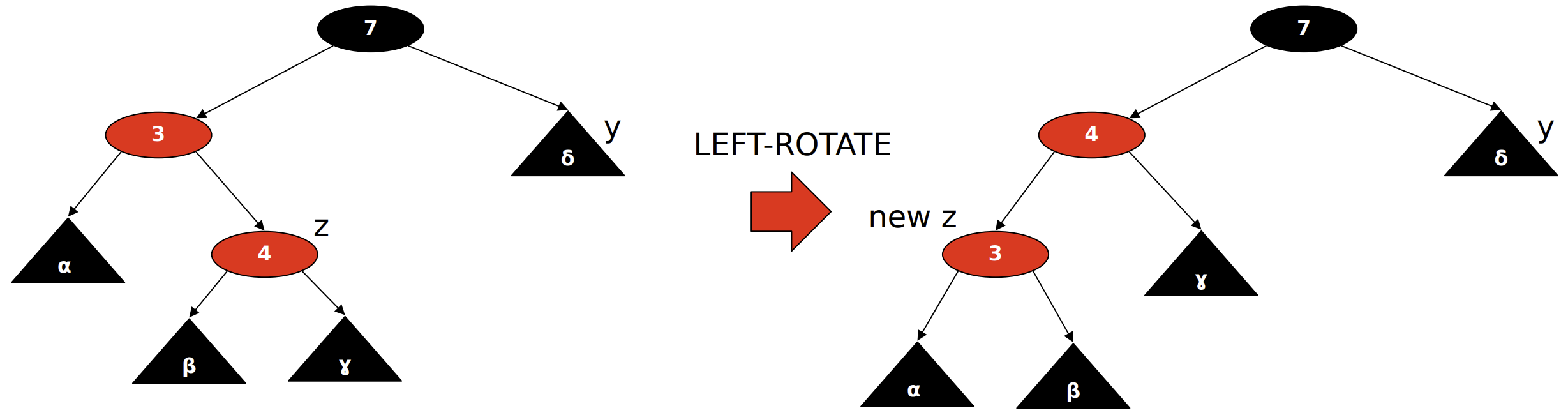
• Case 3: z is a left child and uncle is black → recolor and rotate right.

def FIXUP(T, z):
    while z.p.colour == RED:
        if z.p == z.p.p.left:
            y = z.p.p.right
            if y.colour == RED:
                z.p.colour = BLACK     # case 1
                y.colour = BLACK       # case 1
                z.p.p.colour = RED     # case 1
                z = z.p.p              # case 1
            else:
                if z == z.p.right:
                    z = z.p            # case 2
                    LEFT-ROTATE(T, z)  # case 2
                z.p.colour = BLACK     # case 3
                z.p.p.colour = RED     # case 3
                RIGHT-ROTATE(T, z.p.p) # case 3
        else:
            # Symmetric cases if z.p is right child
            ...
    T.root.colour = BLACK

Advantages of Red-Black Trees

• Fast insertion and deletion: fewer rotations compared to AVL_tree.
• Balanced height: worst-case O(log n).
• Widely used: e.g., Linux scheduler, Java TreeMap, STL map.

Footnotes

1. : 1.Every node is either red or black 2. The root is black 3. Every leaf (NIL) is black 4. If a node is red, then both its children are black 5. For each node, all simple paths from the node to descendant leaves contain the same number of black nodes ↩