functions

A function is a mapping from elements of set $x$ to elements of set $y$ $f:\mathbb{R}\to \mathbb{R}$

domain

The set of all possible input values for which the function is defined.

codomain

The set of all possible output values that the function can produce.

Function Types

Increasing/Decreasing

consider the function $f:\mathbb{R}\to \mathbb{R}$ $f$ is strictly increasing if $x_1<x_2$ , then $f(x_1)<f(x_2)$ $f$ is strictly decreasing if $x_1>x_2$ , then $f(x_1)>f(x_2)$ !! A strictly increasing/decreasing function must be injective

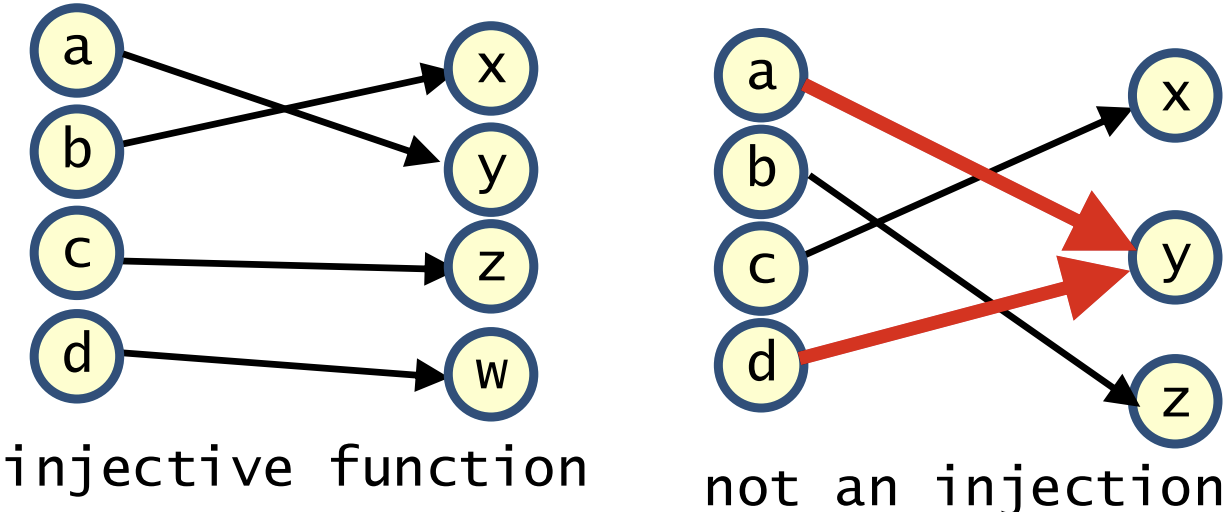
Injective

a one-to-one mapping of the domain to codomain $\forall x_1\in X.\forall x_2\in X.(x_1\ne x_2\to f(x_1)\ne f(x_2))$ $or$ $\forall x_1\in X.\forall x_2\in X.(f(x_1)=f(x_2)\to x_1=x_2)$

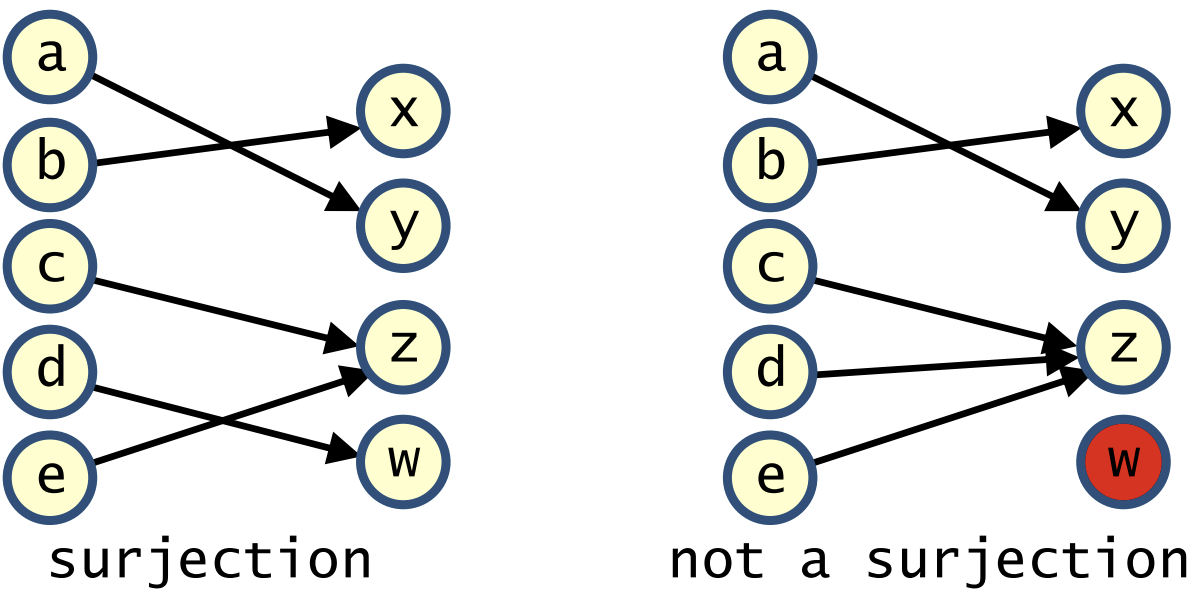
Surjective

a onto mapping, means every element in the codomain has at least one preimage^[preimage : the original input value(s) from the domain that map to a given output value in the codomain under a function.] in the domain. $\forall y\in Y.\exists x\in X.(f(x)=y)$

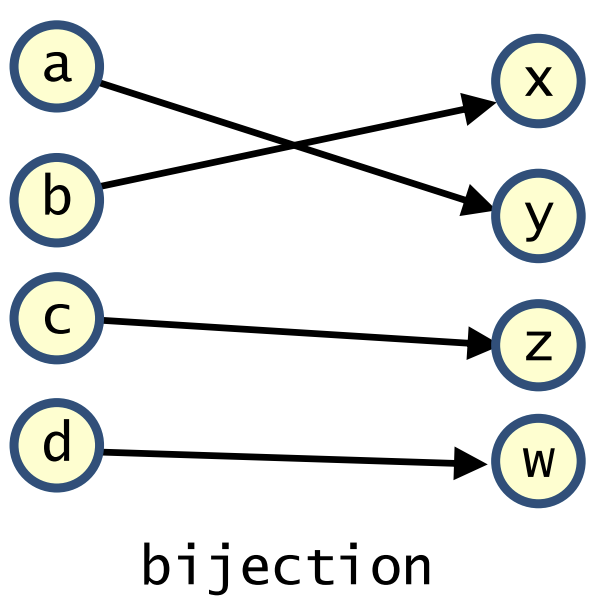
Bijective

if function $f$ is bijective it is both Injective and Surjective:

• maps different elements of the domain to different elements of the codomain
• each element of codomain has a preimage

Inverse

for an inverse of a function to exist there must be a Bijection. The inverse of a function Undos the mapping of the Original function.

Inverse function Properies

for the function $f:X\to Y$ $(f(f^{-1}(y))=y)\forall y\in Y$ $(f^{-1}(f(x))=x)\forall x\in X$