Binary Tree

A binary tree is a linked data structure in which each node x has an attribute key and three pointer attributes

• x.p points to its parent
• x.left points to its left child
• x.right points to its right child
• The root of the tree is the only node whose parent is NIL
• Node x is a leaf when x.left = x.right = NIL Given a tree T
• T.root points to the root element of tree T
• If T.root = NIL, the tree is empty

The height (h) of a tree is the length of the longest path from the root These trees can be traversal in different ways.

Left subtree	Right subtree

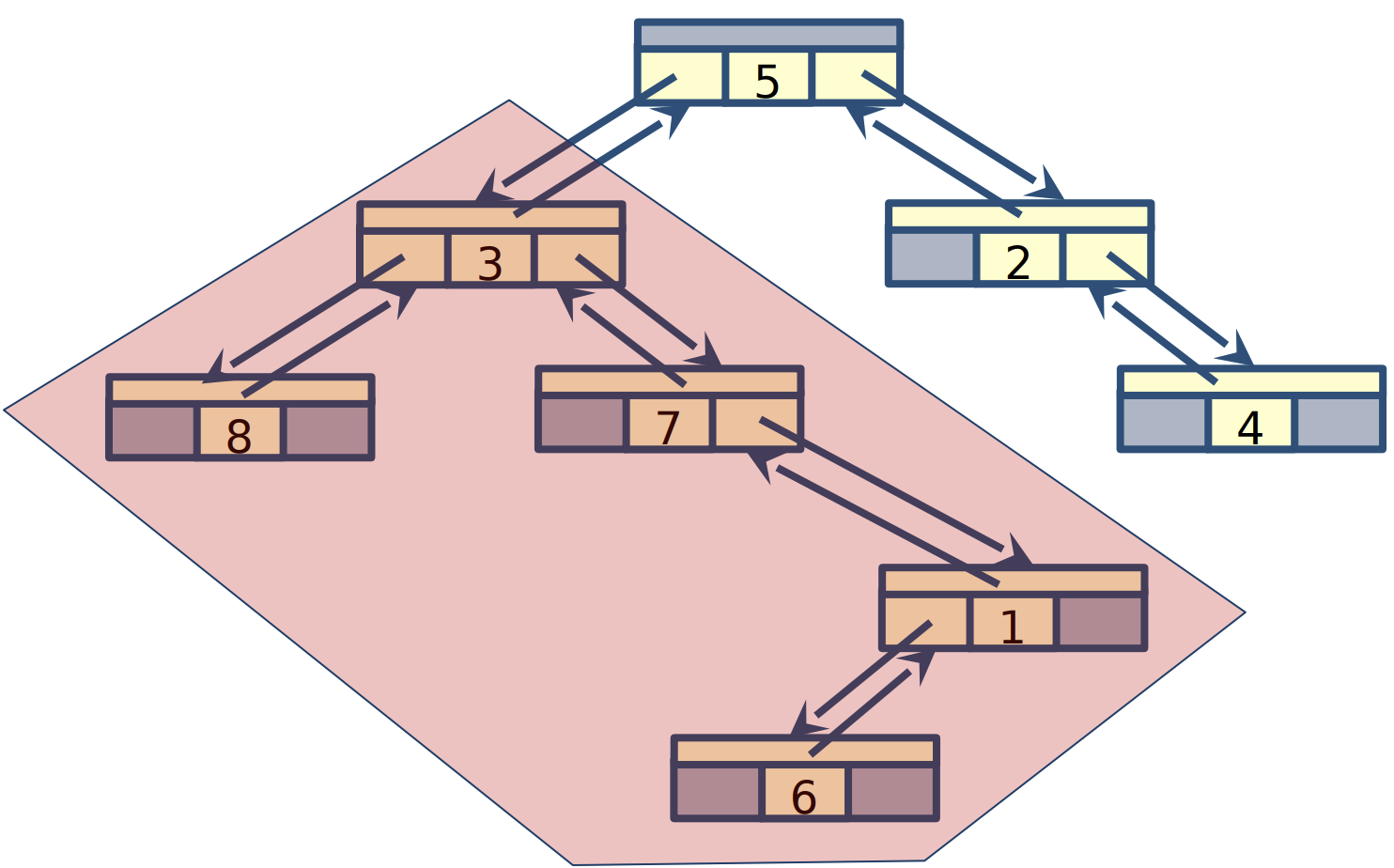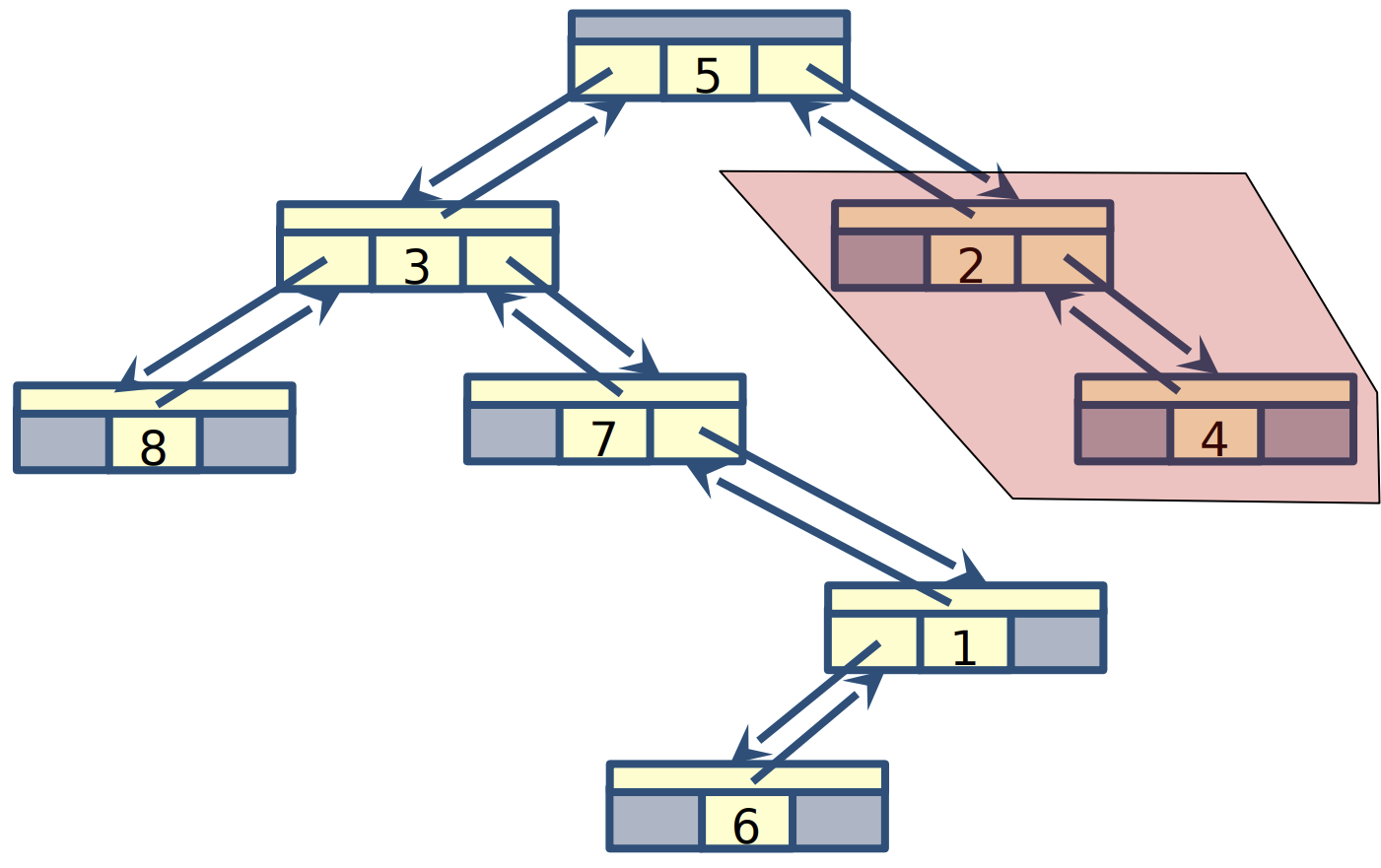Path from 3 to 6:

• 3,7,1,6 = length 3

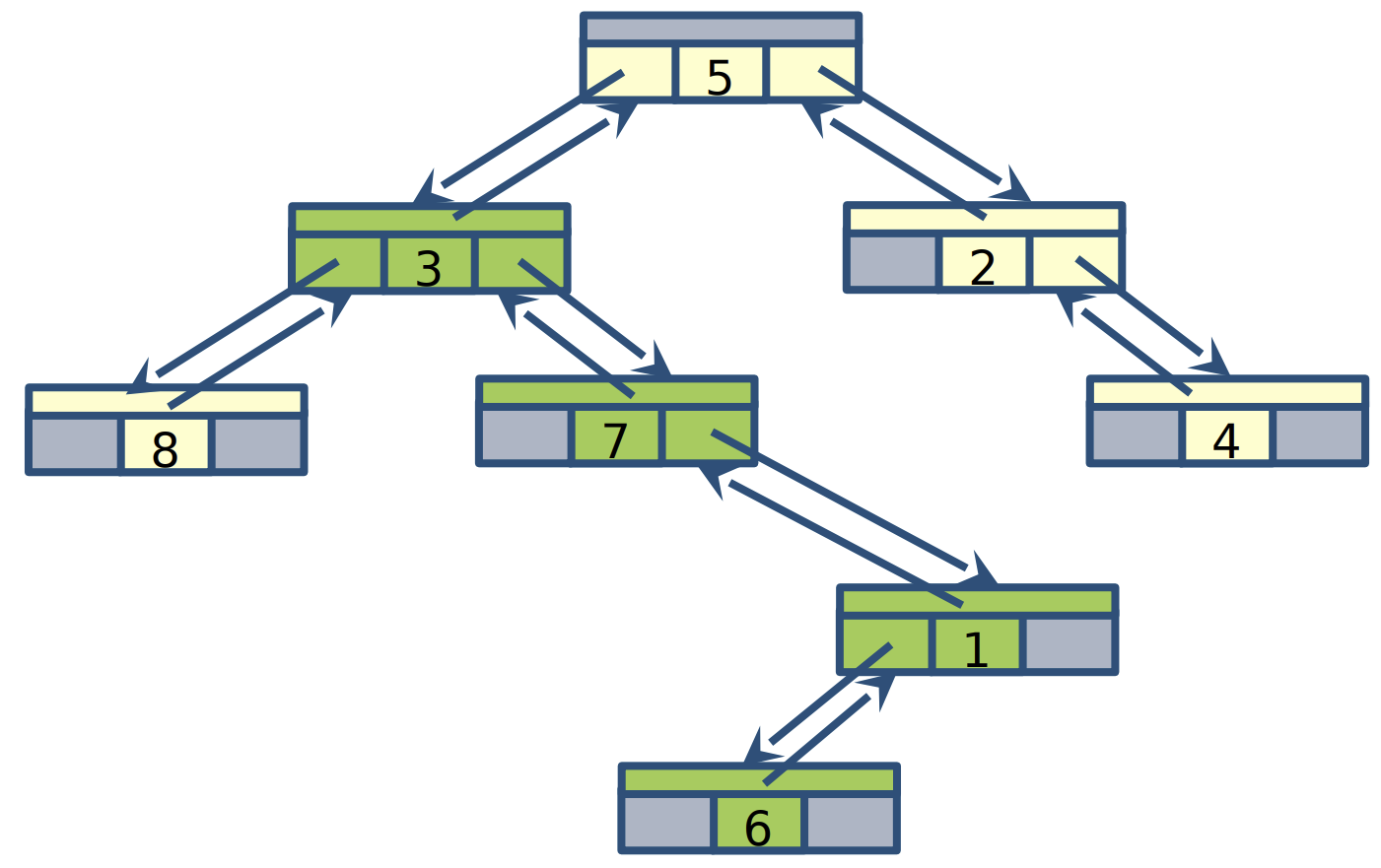
Balanced trees

a balanced binary tree is a binary tree in which the left and right subtrees of every node differ in height by no more than 1

• Height $O(logn)$

k-array trees

Trees with a bounded number of children (k-array trees) can be easily represented with additional pointer attributes $chil{d}_1,\dots ,chil{d}_k$

Limitations

• A lot of NIL values if many nodes have less than k children
• k is fixed (it needs to be known in advance)

unbounded branching

Trees with an unbounded number of children can easily be represented with additional attributes

• x.left-child points to the leftmost child of x
• x.right-sibling points to the sibling of x immediately to its right

Limitations

• Accessing a child is O(k) as we need to scan all the list of children to access the rightmost child
• k is the maximum branch degree