map

A map models a searchable collection of key/value pairs

• Multiple entries with the same key are not allowed (keys must be unique)

Operations

Main map operations

• INSERT(M,k,v): add a pair (k,v) to map M
• DELETE(M,k): remove key k and its value from map M
• SEARCH(M,k): find a pair with key k in map M

Auxiliary map operation

• MAP-EMPTY(M): test whether no key/value pairs are stored in map M

Implementation

List-based

We can implement a map M using an unsorted doubly-linked list

Performance

• INSERT takes O(1) time (O(n) if we first check for duplicates)
• SEARCH/DELETE take O(n) time since in the worst case (the item is not found) we traverse the entire list to look for an item with the given key The list-based implementation is efficient only for maps of small size

Tree-based

Self-balancing trees guarantee a worst-case time complexity of O(log n) for all the main operation of the Map ADT

• inorder traversal allows us to get a sorted sequence of all the pairs stored in the map

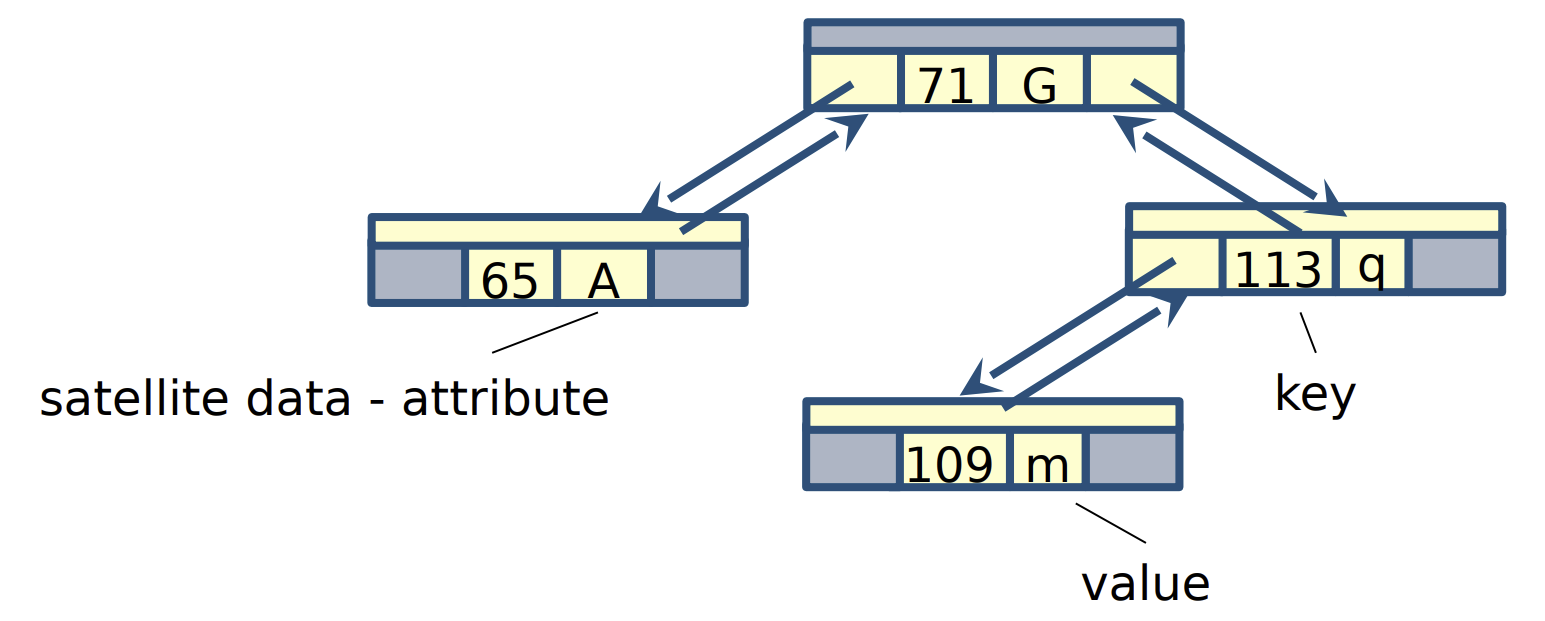
Direct Access Table

We use an array or direct-address table T[0,..,m - 1] to represent the map

• Each position (also called slot or bucket) in T corresponds to a key in the universe U
• Slot k points to to an element in the map with key k
• If no element has key k, then T[k] = NIL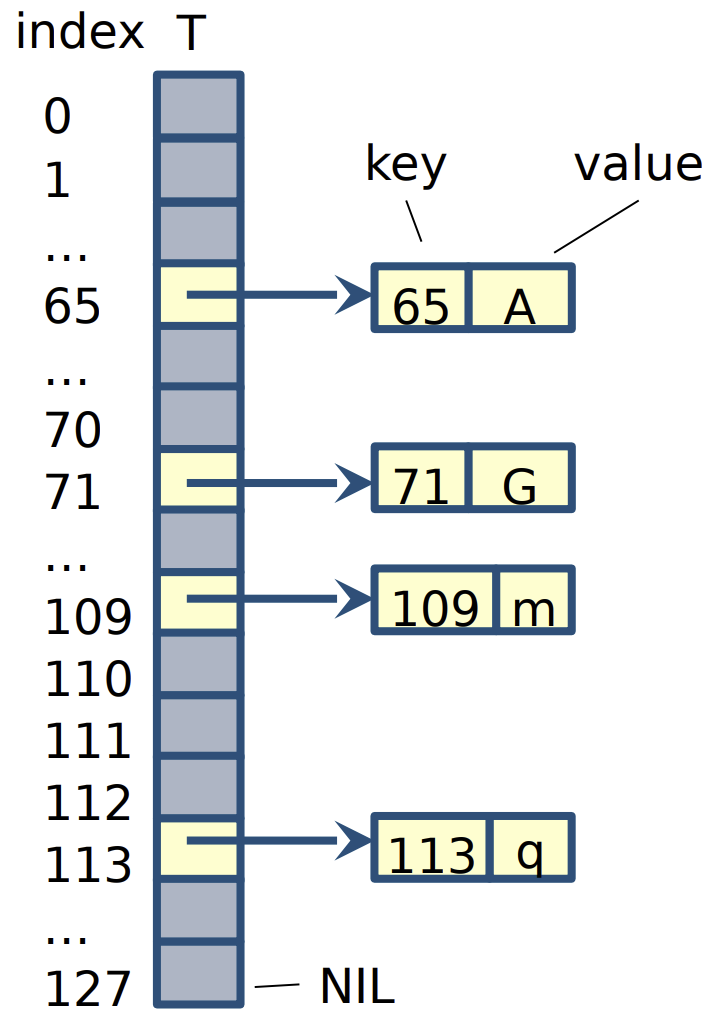

Operations

Each operation takes O(1) time The best time for any implementation