Recursion

A function is recursive if it refers to itself in its definition. When calling itself, a recursive function makes a clone and calls the clone with appropriate parameters. A recursive algorithm must always:

• reduce size of data set, or the number its working on, each time it is recursively called
• provide a stopping case (terminating condition)

Recursion has a cost - The memory usage to keep track of the state of each recursive call Non-recursive algorithm are also called iterative

Recursion Visualization

Recursive Trace

Graphical method to visualize the execution of recursive algorithms Drawn as follows:

• A box for each recursive call
• An arrow from each caller to callee (in black)
• An arrow from each callee to caller showing return value (in blue) (we will often omit this)

Fact(n):
	if n == 1:
		return 1
	else:
		return n * Fact(n-1)
# highly inefficent only for demonstation purposes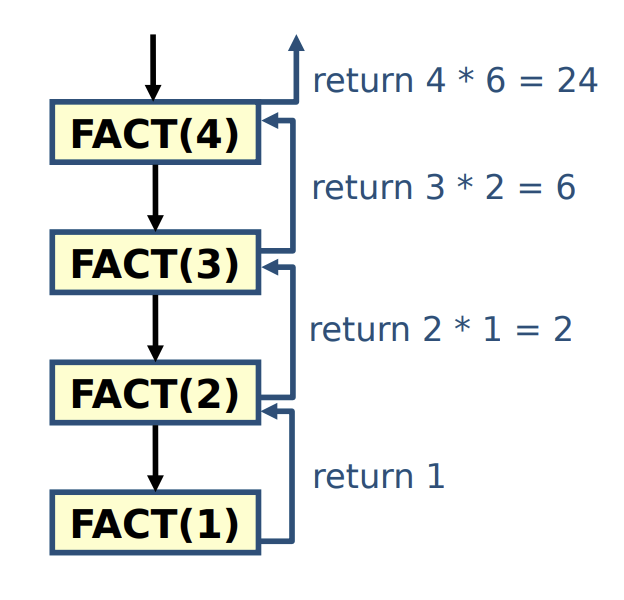

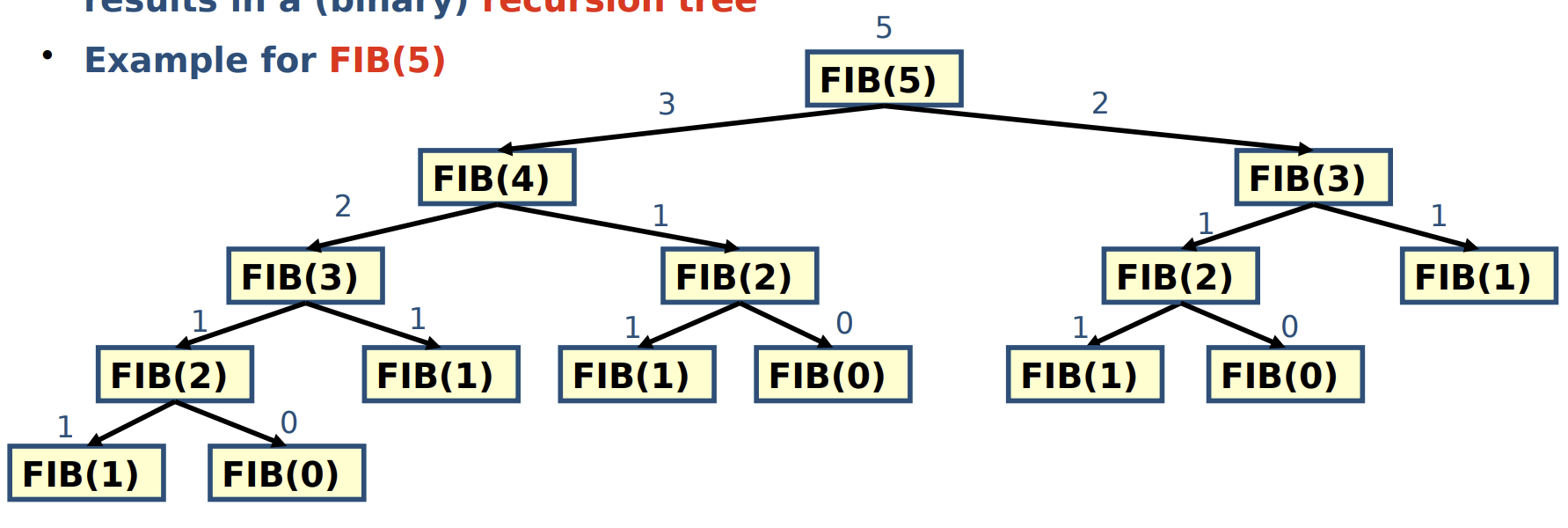
Recursion Tree

Visualizing each recursive call in an algorithm using binary recursion results in a (binary) recursion tree

• The number of nodes $n$ in a full binary tree is at most $n=2h+1-1$ where $h$ is the height of the tree

Types of Recursive functions

Linear Recursion

linear recursion a method is defined so that it makes at most one recursive call each time it is invoked. The amount of space needed to keep track of the nested calls, grows linearly with n

Tail Recursion

An algorithm uses tail recursion when recursion is linear and recursive call is its very last operation Algorithms using tail recursion can be converted to a non-recursive algorithm by iterating through recursive calls rather than calling them explicitly

Binary Recursion

When an algorithm makes two recursive calls, we say that it uses binary recursion

def Fib(n):
	if n <= 1:
		return n
	else:
		return Fib(n-1) + Fib(n-2)