Connectives

used to generate new mathematical statements from combining one or more Propositions. These are called compound propositions or Compound_Propositions. Truth tables will be used to display the relationship between a formula and the propositions within it.

Notation

• connectives : P,Q,R,etc

Types

Negation (¬) not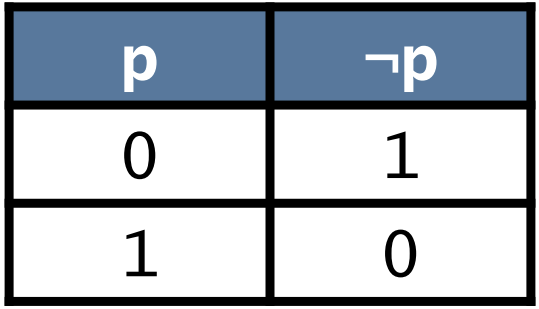
Conjunction(∧) and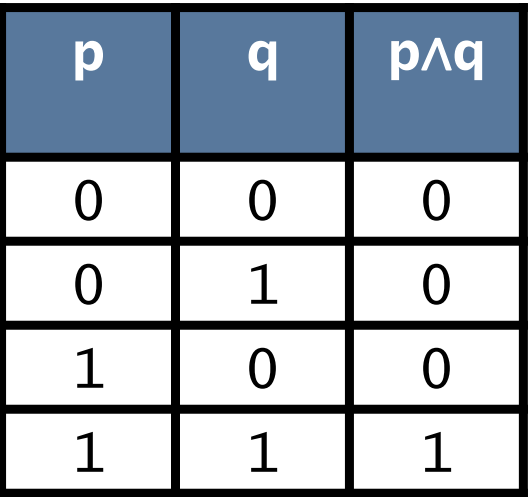
Disjunction(∨) or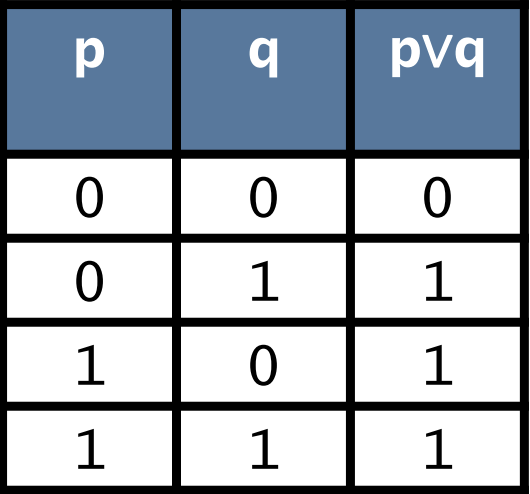
Exclusive Or(⊕) xor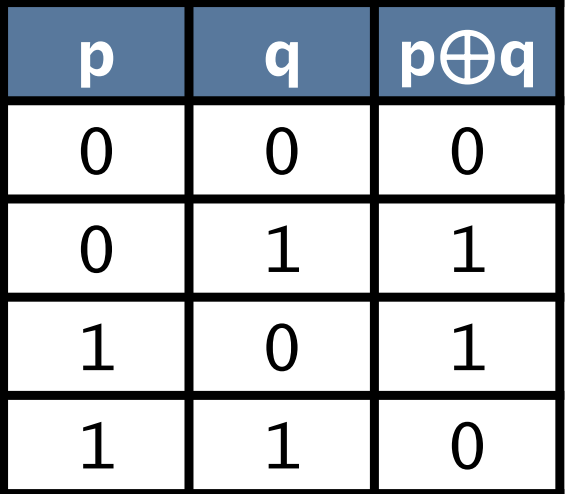
Implication(➝) implies Logically equivalent - base : p➝q - contrapositive : ¬q➝¬p -------------------- Logically equivalent - converse : q➝p - inverse : ¬p➝¬q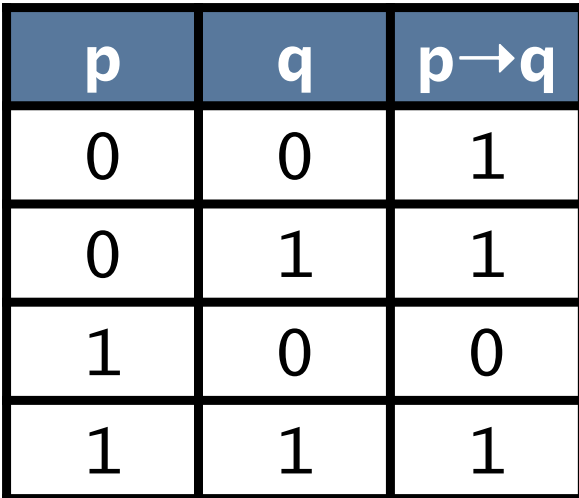
Biconditional( ⟷) if and only if

Precedence

a propositions order of connectives matter.

• order:
  • ∧
  • ∨
  • ➝
  • ⟷